Ich habe mein Mathe-Abitur erfolgreich bestanden und nun studiere ich Medien-Informatik. Das erste Mal, seit ich sie geschrieben habe, schaue ich mir die Prüfungsaufgaben an. Ich versuche hier die Aufgaben mit Hilfe von Sage zu lösen. Dies ist zum Einen eine Auffrischung, ob ich noch weiß, was ich aus mathematischer Sicht mache aber auch eine Übung bzw. ein Beispiel, wie man mit Sage seine Mathe-Aufgaben lösen kann.
In Code-Tags eingefasste Statements sind Sage-Code. Das Worksheet ist unten zum Download angehängt.
Die Grund-Aufgabe
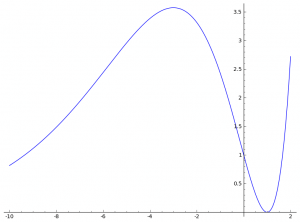
Gegeben ist folgende Funktion: $latex y=f_t(x)=e^{tx}(x-1)^2 ~~~~~ (x \in R) ~~~~~ (t \in R, t > 0) &bg=000000&fg=ffffff$
Außerdem ist diese Funktion, für alle weiteren Aufgaben, im Intervall von -10 bis 2 gezeichnet (beides einschließlich). Das sieht so aus:
Teilaufgabe a:
Es soll die erste Ableitungsfunktion angegeben werden, sowie Nährungswerte für die Nullstellen, alle x für welche die Ableitung negativ ist und die Anzahl der Extremstellen.
Die Ableitung geben wir so an:
[cce lang=“python“]var(‚t x‘);
assume(t>0);
f=(e^(x*t))*(x-1)^2;
fd = derivative(f,x);
show(fd);[/cce]
[latex]{\left(x – 1\right)}^{2} t e^{\left(t x\right)} + 2 \, {\left(x – 1\right)} e^{\left(t x\right)}[/latex]
Die Restlichen Teilaufgaben sollen eher geschätzt werden. Die der Ableitung sind bei -3 und 1. Das sind die beiden Extremstellen. Und die Ableitung ist zwischen -3 und 1 negativ. Dort, wo die Funktion abfällt.
Teilaufgabe b:
Es existiert genau eine Wendetangente an den Graphen der Funktion f2 die mit dem Graphen von f2 eine Fläche vollständig begrenzt. Ermitteln Sie einen Näherungswert für den Inhalt dieser Fläche.
[cce lang=“python“]f2 = f(t=2);
#show(plot(f2, xmin=-2, xmax=2, ymax=2.5, ymin=-0.5));
wendestellen = map(lambda a: a.right(), solve(0==derivative(f2,x,2),x));
#show(wendestellen);
anstiege = map(lambda w: derivative(f2,x)(x=w), wendestellen);
#show(anstiege);
funktionswerte = map(lambda w: f2(x=w), wendestellen);
#show(funktionswerte);
wendetangenten = map(lambda m,y,v: (x-numerical_approx(v))*numerical_approx(m)+numerical_approx(y), anstiege, funktionswerte, wendestellen);
#show(wendetangenten);
#show(plot(wendetangenten, xmax=1.5) + plot(f2,xmax=1.5));
korrektetangente = wendetangenten[0]; #Muss manuell ausgewählt werden, da sage für beide Tangenten jeweils zwei Schnittpunkte mit f2 zeigt
#show(korrektetangente);
diff = f2-korrektetangente;
#show(diff);
nst1 = find_root(diff==0,-10,0); #Diese Lösungen müssen numerisch gefunden werden, da die Gleichung nicht symbolisch lösbar ist
nst2 = find_root(diff==0,0,10);
show(abs(integrate(diff,x,nst1,nst2)));[/cce]
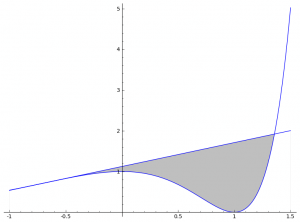Die Lösung: 1.29480589847
Interessanterweise kann diese Aufgabe nicht ohne Taschenrechner gelöst werden, da spätestens das Finden der Schnittstellen zwischen Tangente und Graph nicht mehr symbolisch funktioniert. Das ist auch der Grund, warum die korrekte Tangente (die der ersten Wendestelle, was offensichtlich ist) manuell gewählt werden muss.
Teilaufgabe c:
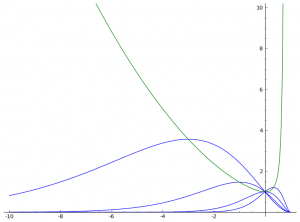Es soll die Funktion g gefunden werden, auf der die lokalen Maxima der Funktionen ft liegen. Wir suchen nochmal die entsprechende Maximalstelle.
extremstellen = solve([derivative(f,x)==0],x);
fdd = derivative(f,x,2);
maximastelle = filter(lambda d: len(solve([fdd(x=d.right()) < 0],t)) > 0, extremstellen)[0].right();
#show(maximastelle);
maximawert = f(x=maximastelle);
#show(f);
tparam = solve([x==maximastelle],t)[0].right();
g=(maximawert(t=tparam));
show(factor(g));
Folgende Funktion kommt dabei raus: [latex]{\left(x – 1\right)}^{2} e^{\left(-\frac{2}{x – 1} – 2\right)}[/latex]
Teilaufgabe d:
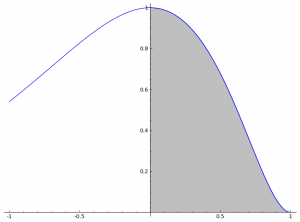Gezeigt werden soll, dass [latex]F_2(x) = \frac{1}{4} \, {\left(2 \, x^{2} – 6 \, x + 5\right)} e^{\left(2 \, x\right)}[/latex] eine Stammfunktion von f2 ist. Außerdem soll der korrekte Flächeninhalt, der von f2 und den Koordinatenachsen eingeschlossen ist, errechnet werden.
F2 = 1/2 * e^(2*x) * (x^2 - 3*x + 5/2);
show(bool(F2 == integrate(f(t=2),x))); # True
show(plot(f(t=2), fill=True,xmin=0) + plot(f(t=2)));
# Die Nullstelle ist eigentlich bekannt, aber wir errechnen sie noch mal
nst = solve(f(t=2),x)[0].right();
show(integral(f(t=2),x,0,nst));
Ergebnis: [latex]\frac{1}{4} \, e^{2} – \frac{5}{4}[/latex]
Teilaufgabe e:
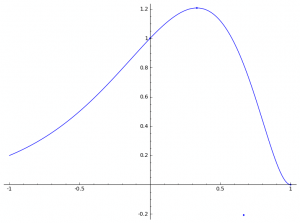Die Extrempunkte und die Schnittpunkte mit den Koordinatenachsen von f3 bilden gemeinsam ein Dreieck. Zu finden sei ein vierter Punkt, der ein vollständiges Parallelogramm aus diesen Punkten macht.
extremstellen = solve(derivative(f(t=3),x)==0,x);
dreieck = [];
dreieck.extend(map(lambda y: vector([y.right(),f(t=3,x=y.right())]) ,extremstellen));
dreieck.append(vector([0,f(t=3,x=0)]));
dreieck.append(dreieck[2] + (dreieck[1]-dreieck[0]));
show(dreieck[3]);
show(plot(list(point((d[0],d[1])) for d in dreieck)) + plot(f(t=3)));
Und es stellt sich heraus, dass einer der möglichen Parallelogramm-Punkte folgender ist: [latex]\left(\frac{2}{3},\,-\frac{4}{9} \, e + 1\right)[/latex]
Teilaufgabe f:
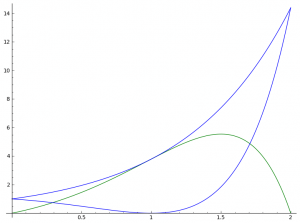Und als letzte Analysis Aufgabe: Für jedes t ist eine Funktion ht wie folgt definiert: [latex]h_t(x) = e^{tx}[/latex]. Für jeden Wert existiert genau ein Wert u, für den Differenz der Funktionswerte ht(x)-ft(x) an der Stelle x=u (und u zwischen (ausgeschl.) 0 und 2) maximal wird. Ermitteln Sie den Wert t, für den u=3/2 ist.
var('u');
assume(0 < u < 2);
h = e^(t*x);
diff = h(x=u)-f(x=u);
ddiff = derivative(diff,u);
show(solve([ddiff(u=3/2)==0],t));
Und da kommt folgendes raus: [latex]\left[t = \left(\frac{4}{3}\right)\right][/latex]
Und damit hätten wir den ersten Teil, Analysis, schon gelöst. Einfach hier klicken, um das Worksheet runterzuladen und selbst auszutesten.
- Teil 1: Analysis
- Teil 2: Algebra (folgt)
- Teil 3: Stochastik (folgt)
- Wahlteil 1 (folgt)
- Wahlteil 2 (folgt)